« パスタ!パスタ!パスタ! | メイン | トマトとアイスクリームのカラメルソースがけ »
2006年06月18日
雨降りでなるべく濡れない方法は?(その3)
「傘を持たず雨の中を家まで帰るとき、本当に走って帰ったほうが濡れないのか?」と言う問題の続きです。
前回までのお話はこちら。
前回は、次の式を求めたところで終わっていました。
体に当たる雨粒の数 = 雨の密度 × 雨の相対速度 × 雨の相対速度方向から見た体の面積 × 時間
今回は、この式から、どんな速度で帰れば一番濡れないのかを求めてみます。
まずは、既知のパラメータをリストアップしましょう。
d 家までの距離 ρ 雨の密度 Vr 雨の速度(真下方向)の大きさ Vw 人の歩行速度(水平方向)の大きさ la 人(直方体)の前後方向の長さ lb 人(直方体)の上下方向の長さ lc 人(直方体)の左右方向の長さ
これらのパラメータを材料に、体に当たる雨粒の数を計算するわけです。
d と ρ 以外を絵で説明するとこんな感じになります。
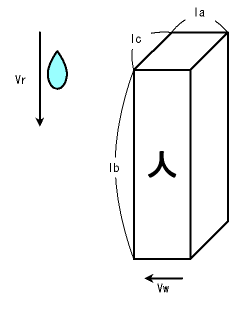
冒頭の式の右辺のうち、「雨の密度」は ρ 、(家に着くまでの)「時間」は d / Vw とすぐに求まります。残りの「雨の相対速度」(Vrel)と「雨の相対速度方向から見た体の面積」(Srel)を求めてみましょう。
「雨の相対速度」(Vrel)は Vr と Vw から次の図のように求められ、
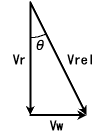
Vrel の大きさは、 ![]() と計算できます。
と計算できます。
そして、「雨の相対速度方向から見た体の面積」(Srel)は、人(直方体)の各辺の長さと雨の相対速度の角度θから、次のような図が描け、
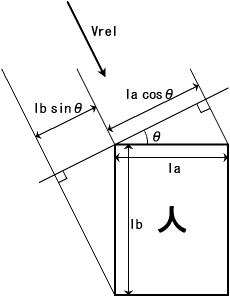
このように求まります。
そして、cosθ と sinθ は、Vr と Vw を使って
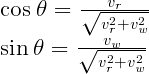
と書けるので、Srel は
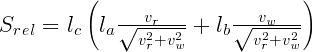
と書き直せます。
さて、最初の式の右辺の要素が全て既知のパラメータの式で書けたので、それらの式を総合すると、「体に当たる雨粒の数」(R) は、次のようになります。
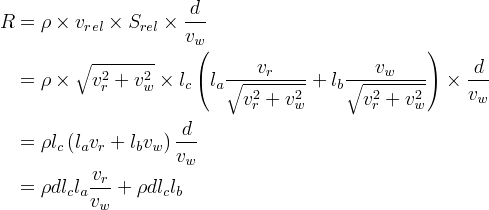
この式から、「どんな速度(Vw)で帰れば一番濡れないか」を考えるわけですが、どう見ても Vw が大きいほど「体に当たる雨粒の数」(R)は小さくなりますね…
「走って帰ろうが、歩いて帰ろうが、雨に濡れる量は同じ」なのではないか?そうだったら意外で面白いなーってとこから始まったこの考察ですが、「速ければ速いほど濡れない」という、意外でもなんでもない拍子抜けな結果になってしまいました。LaTeX使って式を書いてみたり、Dynamic Drawで図を描いてみたり、がんばったわりには実りが少なくてガッカリです。世の中、面白いことなんてそうそう無いってことでしょうか。はぁ~っ。
まー、どんなつまらないことでも自分でちゃんと確かめてみることが大事なんですよ、って理屈で自分をなぐさめつつ、今回の結論!
結論:「雨に濡れたくなければ走って帰れ」投稿者 sike : 2006年06月18日 04:58
トラックバック
このエントリーのトラックバックURL:
http://ashiato.jp/mt33/mt-tb.cgi/95
コメント
ううう、もうその方程式を見ただけで気がふれる。
とりあえず雨の日は髪の毛が爆発するのでイヤだ。
あーあと子供の頃雨に濡れるとハゲるとか皮膚がただれるとか言ってた。チェルノブイリのやつ。子供ってバカだよね。(自分を思い返して)
投稿者 ひめお : 2006年06月19日 23:31
あれ?濡れたくなければ早く走れば良いの??中学時代の数学の先生の解は間違ってたのかな?そもそも、例題の出し方が何からだったかも忘れてますがw
いやー、でもなんですか、この呪文のような数式は。sikeさんはすごいなー。プログラマーは万能ですよ。魔法使いですよホント。ど
投稿者 船長 : 2006年06月23日 01:21
ううう、数学、嫌われ者ですね…
記号が沢山あるから呪文のように見えるのかな?
大した計算やってないんですけどねー。
チェルノブイリもそうだけど、酸性雨で木が枯れてるとかで、禿げるとか、そういう噂ありましたねー。
ちなみに、僕は、雨が降るとベランダのトマトの育ちが悪くなるのでイヤです。
投稿者 sike : 2006年06月23日 03:24
数学、それ自体がどうというより、生き残り(受験)優先で勉強するしかない脳みその持ち主な僕は、心にゆとりもなく、暗記すれば点が取れるとか、少しでも偏差値上げる為には攻めやすい教科から勉強するとかそういう所が縁を遠ざけた原因かな~とか。いきなり、スペイン語並べられてもなんじゃこりゃ~っ!!ってのと同じですよ、タブン。
チェルノブイリ、僕は、幼児の頃、第五福竜丸の被爆事件があって、雨の日ずぶぬれで遊んでいたら、放射能に汚染されると母に怒られた記憶がある。ジェネレーションが…orz
投稿者 船長 : 2006年06月27日 12:55