2006年12月14日
三角関数の多項式近似の係数
コンピュータで sin の計算をするときって、テイラー展開を低次の項で打ち切った多項式近似って感じの計算をしてるわけなのですが、その係数の求め方がよくわからん。
sin を テイラー展開(マクローリン展開?)すると、こんな感じになるでしょ。
sin(x) = x - x3/3! + x5/5! - x7/7! + x9/9! - ...
で、newlib の sinf の実装を見てみると、9次の項までを使った多項式近似になってて、こんな係数を使ってるんよね。
static const float r[] = {
-0.1666665668, /* -1/3! = -0.1666666666... */
0.8333025139e-02, /* 1/5! = 0.8333333333...e-02 */
-0.1980741872e-03, /* -1/7! = -0.1984126984...e-03 */
0.2601903036e-5 /* 1/9! = 0.2755731922...e-05 */
};
コメントに書いたのがテイラー展開したときの係数なのだけど、実際に使われている値と違うでしょ?多分、精度を上げるためにこんな係数を使っているのだと思うのだけど、どうやってこれを求めたのかが良く分からない。最小二乗法とかで求めるの?誰か知らない?
投稿者 sike : 01:43 | コメント (2) | トラックバック
2006年10月22日
Color Illusion
下の画像の上にマウスポインタを置いてください。どぎつい色の画像が表示されると思います。
その状態で約30秒じっと画像を見つめてください。(黒い点を見つめると良いかも)
そして、視線を動かさないままマウスポインタを画像の上からどけてください。
再び白黒画像が表示されるはずなのですが、目の錯覚で色がついて見えます。

補色を利用した錯覚のようです。
元ネタは Color Illusion Tutorial。Photoshopでこのような画像を作るための手順が書いてあります。
Photoshopなんてブルジョワソフトは持ってない人は GIMP for Windows などを使いましょう。当然僕も持ってません。
GIMPの場合、白黒画像は、メニューから 「レイヤー → 色 → 脱色」で作れます。
もう一枚の画像は、塗りつぶしツールで 「モード」を「明度」 にして 50%グレー で塗りつぶし、さらにメニューから 「レイヤー → 色 → 反転」で作れます。
正確には明度じゃなくて輝度に基づいた画像変換をしないといけないと思うのですけど、手順が複雑になるので省略。
この手順でもそれなりに見えると思います。
(ちなみに、上の猫画像は輝度方式で作ったつもり。)
追記
GIMPで画像を加工する手順のフラッシュを作ってみました。
(Winkで作りました)
投稿者 sike : 19:27 | コメント (0) | トラックバック
2006年06月18日
雨降りでなるべく濡れない方法は?(その3)
「傘を持たず雨の中を家まで帰るとき、本当に走って帰ったほうが濡れないのか?」と言う問題の続きです。
前回までのお話はこちら。
前回は、次の式を求めたところで終わっていました。
体に当たる雨粒の数 = 雨の密度 × 雨の相対速度 × 雨の相対速度方向から見た体の面積 × 時間
今回は、この式から、どんな速度で帰れば一番濡れないのかを求めてみます。
まずは、既知のパラメータをリストアップしましょう。
d 家までの距離 ρ 雨の密度 Vr 雨の速度(真下方向)の大きさ Vw 人の歩行速度(水平方向)の大きさ la 人(直方体)の前後方向の長さ lb 人(直方体)の上下方向の長さ lc 人(直方体)の左右方向の長さ
これらのパラメータを材料に、体に当たる雨粒の数を計算するわけです。
d と ρ 以外を絵で説明するとこんな感じになります。
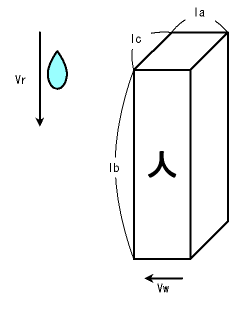
冒頭の式の右辺のうち、「雨の密度」は ρ 、(家に着くまでの)「時間」は d / Vw とすぐに求まります。残りの「雨の相対速度」(Vrel)と「雨の相対速度方向から見た体の面積」(Srel)を求めてみましょう。
「雨の相対速度」(Vrel)は Vr と Vw から次の図のように求められ、
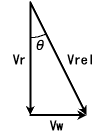
Vrel の大きさは、 ![]() と計算できます。
と計算できます。
そして、「雨の相対速度方向から見た体の面積」(Srel)は、人(直方体)の各辺の長さと雨の相対速度の角度θから、次のような図が描け、
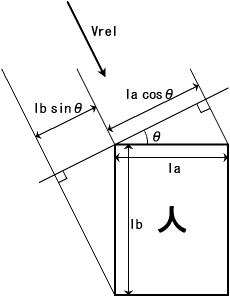
このように求まります。
そして、cosθ と sinθ は、Vr と Vw を使って
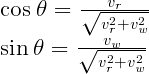
と書けるので、Srel は
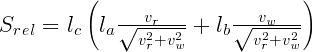
と書き直せます。
さて、最初の式の右辺の要素が全て既知のパラメータの式で書けたので、それらの式を総合すると、「体に当たる雨粒の数」(R) は、次のようになります。
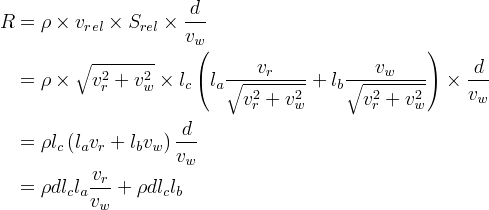
この式から、「どんな速度(Vw)で帰れば一番濡れないか」を考えるわけですが、どう見ても Vw が大きいほど「体に当たる雨粒の数」(R)は小さくなりますね…
「走って帰ろうが、歩いて帰ろうが、雨に濡れる量は同じ」なのではないか?そうだったら意外で面白いなーってとこから始まったこの考察ですが、「速ければ速いほど濡れない」という、意外でもなんでもない拍子抜けな結果になってしまいました。LaTeX使って式を書いてみたり、Dynamic Drawで図を描いてみたり、がんばったわりには実りが少なくてガッカリです。世の中、面白いことなんてそうそう無いってことでしょうか。はぁ~っ。
まー、どんなつまらないことでも自分でちゃんと確かめてみることが大事なんですよ、って理屈で自分をなぐさめつつ、今回の結論!
結論:「雨に濡れたくなければ走って帰れ」投稿者 sike : 04:58 | コメント (4) | トラックバック
2006年06月10日
雨降りでなるべく濡れない方法は?(その2)
雨は真下にふると仮定します。人が止まっているとすると雨は真上からだけ当たります。
その場合、体に当たる雨粒の数は、
体に当たる雨粒の数 = 雨の密度 × 雨の速度 × 真上から見た体の面積 × 時間で良い気がします。
納得できないなら、上の開いた1辺1mの立方体の箱が雨の中に放置されているところを想像してください。 雨の密度が100個/m3だとすると、ある瞬間に箱の中には雨粒が100個あります。 雨の速度が1m/秒(雨粒が1秒かけて1m落ちる)だとすると、ある瞬間に箱の中にあった100個の雨粒が1秒後には全て箱の底に当たります。
これを式に直すと、
100 = 100 × 1 × 1 × 1です。 言葉を使った式で言えば、
箱の底に当たる雨粒の数 = 雨の密度 × 雨の速度 × 箱の底の面積 × 時間です。
検証のため、条件を変えて確かめてみましょう。 雨の密度が2倍になれば、底に当たる雨粒の数も2倍になるのは直感的にもわかりますよね? それを式に適用すると、
200 = 200 × 1 × 1 × 1また、雨の速度が2倍になった場合でも、底に当たる雨粒の数が2倍になります。
200 = 100 × 2 × 1 × 1同様に、箱の底の面積が2倍になっても、底にあたる雨粒の数が2倍になりますし、
200 = 100 × 1 × 2 × 1時間が2倍になっても、底にあたる雨粒の数が2倍になります。
200 = 100 × 1 × 1 × 2
さて、人が止まっていると仮定した話をしてきましたが、人が移動してたとしても同じ話ができます。 ただし、雨粒も人も動いているとややこしいので、相対的に考えます。
雨が真下にふっていたとしても、水平に動いている人から見れば雨は斜めに自分に向かってふっているように見えますよね? つまり、人が止まっていて雨が斜めに人に向かってふっていると考えても、雨の当たり方は同じということです。
そう考えた場合、
体に当たる雨粒の数 = 雨の密度 × 雨の速度 × 真上から見た体の面積 × 時間という式は、
体に当たる雨粒の数 = 雨の密度 × 雨の相対速度 × 雨の相対速度方向から見た体の面積 × 時間になります。
この式の右辺の要素のうち、「雨の密度」は歩いて帰ろうが走って帰ろうが一定です(雨が強くなったり弱くなったりすることはないという仮定です)。変化するのは、その他の3つです。
- 「雨の相対速度」は人の速度が速いほど大きくなります。
- 「雨の相対速度方向から見た体の面積」は人が傾かずに移動するとすると(実際は違いますが簡単のため)、速度が速いほど大きくなります。(人は真上から見たほうが横から見るより小さく見える)
- 「時間」は人の速度が速いほど小さくなります。
人の速度が速いほど、大きくなる要素と小さくなる要素がありますね。 簡単にこうすれば一番濡れないとは言えないようですが、人の形を直方体と考え単純化すれば、人の速度と当たる雨粒の数の関数が書けそうな気がしてきました。
やっぱり長くなってきたので、また明日以降に。
投稿者 sike : 15:12 | コメント (0) | トラックバック
2006年06月09日
雨降りでなるべく濡れない方法は?(その1)
小雨の振る中、傘をささず駅からの家路をトコトコと歩きながら考えました。
「雨降りで傘がないとき、濡れたくないから走って帰ったとして、本当に濡れる量は少ないのか?」
仮に、雨の降り方が時間や場所に関係なく一様だとしましょう。
いつでもどこでも、単位体積あたりの雨粒の数が一定だということです。
雨にどれだけ濡れるかというのは、体に当たる雨粒の数で決まるわけですが、それはつまり、「雨に濡れる量は体が通過した空間の体積に比例する」ということではないでしょうか?
そうだとすると、走って帰ろうが歩いて帰ろうが体が通過する体積は一緒なので、どう帰ろうが雨に濡れる量は同じ!
とか思ったけど、今、冷静になって考えてみると、そんなわけねーや。
雨粒が空間の中で静止していたらそれは正しいだろうけど、雨は下に向けて移動しています。
極端な話、雨の中にじっと立っていたら、体が通過する体積は増えないけど、どんどん濡れていくわけです。
同居人に、前述の「どう帰っても濡れる量は同じ」説を話してみたところ、「走って帰ると体の前にも雨が当たるから余計濡れるんじゃないの?」という説が返ってきました。
余計に濡れるかどうかはわかりませんが、雨の当たり方が違うというのは僕もなんとなく感じていたところです。
さらに考えてみよう。
材料は、
・雨の中にいる時間が増えれば濡れる量は増えそうだ
・雨の中での移動速度で雨の当たり方は変わりそうだ
といったところです。
が、長くなってきたので、続きはまた明日。
投稿者 sike : 01:34 | コメント (0) | トラックバック
2006年04月21日
サイコロ頼みの問題解決
深夜のフジテレビで、「たけしのコマネチ大学数学科」っていう番組が放送しています。
なかなか楽しい。
前回見たときは、フィボナッチ数列の話。
今回は、モンテカルロ法でした。
モンテカルロ法っていうのは「サイコロを沢山振って問題を解きましょう」というステキに大雑把な数学手法。
モンテカルロ法で円周率を求めるという話はプログラマーなら聞いたことがあるでしょう。
今回の番組で出題されたのは、
「10分間のショーの間に1分だけ水着ショーがありますが、10分の間のいつあるかはわかりません。カメラマンは1分だけ会場に入って撮影をすることができます。カメラマンが水着ショーを撮影できる確率は?」
という問題でした。
解説者の偉い先生曰く、これは「連続確率」と言われる確率の問題の中でも難しい問題だそうだ。
ところで、僕の勤務している会社は社員の人数に対してトイレが少ないんですよ。
トイレに行ってみると誰かが入っているということが多くて困ります。
それである日考えてみた。
「ある会社にはM個のトイレがあり、N人の社員が一日8時間働いています。一人の社員が一日に一回5分間トイレに入るとして、誰かがトイレに入ろうとしたときにトイレが埋まっている確率は?」
まさにトイレの中でそんなことを考えてみたんだけど、これも時間の連続性ってところがネックになって簡単に解ける気がしなかった。
そのとき頭をよぎったのがモンテカルロ法でした。
考えてわからんものはコンピューターにやらせてしまえ。
まだやってないんだけどね。
今日、その番組を見て似た様な事やってて面白かったという話でした。
投稿者 sike : 02:20 | コメント (0) | トラックバック
2006年03月23日
シートベルトをしないと危ない…のかどうかわからない
この話の解答編です。
58%は微妙なので90%に変えます。こういうのは極端にしたほうが考えやすいのです。
「自動車事故による死亡者の90%がシートベルトを締めていませんでした」
そして、具体的な例で考えてみましょう。
・ある地域のある年の自動車事故による死亡者は100人いました
・死亡者100人のうち90人がシートベルトをしていませんでした
・死亡者100人のうち10人がシートベルトをしていました。
うん、別にこれ自体はおかしくない。そういうこともあるでしょう。
ここでおかしいのはデータ自身ではなく、そのデータを見せた意図です。
このデータを更新時講習で出してきた意味は何なのでしょう?
おそらく「万が一事故を起こしてしまったときのために、シートベルトをしていないと危険です」ということが言いたかったのだと思います。その意見には同意します。シートベルトは締めたほうがよいでしょう。
でもよく考えてください。このデータはシートベルトを締めないことの危険性を表わしているのでしょうか?
シートベルトの着用を勧めるならば、シートベルトをしていないほうが死亡確率が高いことを言わなければなりません。
死亡確率 = 死亡者数 ÷ (生存者数+死亡者数)
ですから、死亡確率について述べたいならば、死亡者だけでなく生存者のこともわからなければなりません。
しかし、上のデータでは死亡者のことしか書かれていません。
極端な例ですが、次のような事実があったとしても上のデータと矛盾しません。
・自動車事故の生存者は820人いました
・生存者820人のうち810人がシートベルトをしていませんでした
・生存者820人のうち10人がシートベルトをしていました
そうすると、
・シートベルトをしていない場合の死亡確率は10%(=90÷(810+90))
・シートベルトをしていた場合の死亡確率は50%(=10÷(10+10))
となり、シートベルトをしているほうが死亡確率が高くなってしまいます。
★まとめ★
「自動車事故による死亡者の90%がシートベルトを締めていませんでした」 というだけでは、シートベルトをしないことの危険性を表わしていない。
シートベルト着用を勧めたいなら、シートベルト着用者の死亡確率とシートベルト非着用者の死亡確率を比較せよ。
2006年03月14日
シートベルトをしないと危ない?
この間、運転免許の更新に行ってきました。
日曜日の運転免許センターってもっと混雑しているものだと思っていたのですが、営業時間の終了間際だったせいかガラガラ。あっという間に手続きが完了してしまいました。
更新時講習では、時速40kmで走っているときに急ブレーキをかけると止まるまでに何m進んでしまうとか、夜は見通しが悪いから危ないとか、よくある話を聞かされるのですが、その中に一つ気になる点がありました。
「自動車事故による死亡者の58%がシートベルトを締めていませんでした」
シートベルトをしないと危ない、という趣旨の話の中に出てきたデータです。
6割弱って、微妙な数字ですよね。多いってほどでもないような。
でも、ここで気になったのはその微妙な数字ではありません。
仮に、58%が90%であったとしても、やっぱり何か違和感を感じる。
さてさて、一体何がおかしいのでしょうか?(つづく)